Every Problem Has a Cheat Code
And it's often ignored
Every solution to a coding problem begins with a crucial decision: what’s the best approach? Yet, one of the biggest hints to finding that answer often goes unnoticed—the input constraints, hidden in plain sight.
In coding challenges, there’s a practical rule of thumb: the largest test case should run in about 1 second. This 1-second limit translates to approximately 100 million single-core operations. Why 1 second? This standard comes from competitive programming, where it’s been a benchmark for decades. It also aligns with user expectations—people are generally willing to wait about 1 second for online systems to respond.
Not all tests will run for 1 second. If a problem has 100 test cases, only one or two will involve the maximum input size that could take up to 1 second to run. The others will typically have smaller inputs and complete much faster.
Example
Let’s say you have a problem with input size N. The input constraints tell you that N can go up to 10⁸. You come up with an obvious quadratic solution, but you’re unsure if it’s optimal. You try improving it by sorting the data, reducing the complexity to O(N log N). But is that good enough, you wonder?
No need to wonder.
We can plug the maximum input size 10⁸ into O(N log N). N log N = (10⁸ log 10⁸) is roughly equal to 3×10⁹ (almost three billion operations). That translates to about a 30-second run time for the largest test case—clearly too slow. So, what’s better than O(N log N)? A linear solution.
If you had paid attention to the constraints before starting to solve the problem, you’d immediately recognize that a linear solution is required. This realization would steer you toward approaches where the answer can be found in a single traversal—or at most, a few passes—through the input data. The strategies you’d now consider might include counting, hashing, or a single-pass greedy algorithm.
"When the constraints reveal the path, let your algorithm follow the flow. Efficiency is the harmony between understanding and execution."
— Faangshui Grandmaster Hashi
This approach can be applied to any problem with input constraints. And if the constraints aren’t provided, don’t hesitate to ask your interviewer for them. On Leetcode the constraints are generally correct, but they don’t always require optimal solutions to pass the tests. Sometimes you’ll see follow-up tasks, such as, “Can you solve this problem in O(N log N) time?” where a more optimal solution is possible. However, on platforms like CodeSignal or HackerRank, where actual interviews take place, the constraints are usually strict and solving within the time limits is critical.
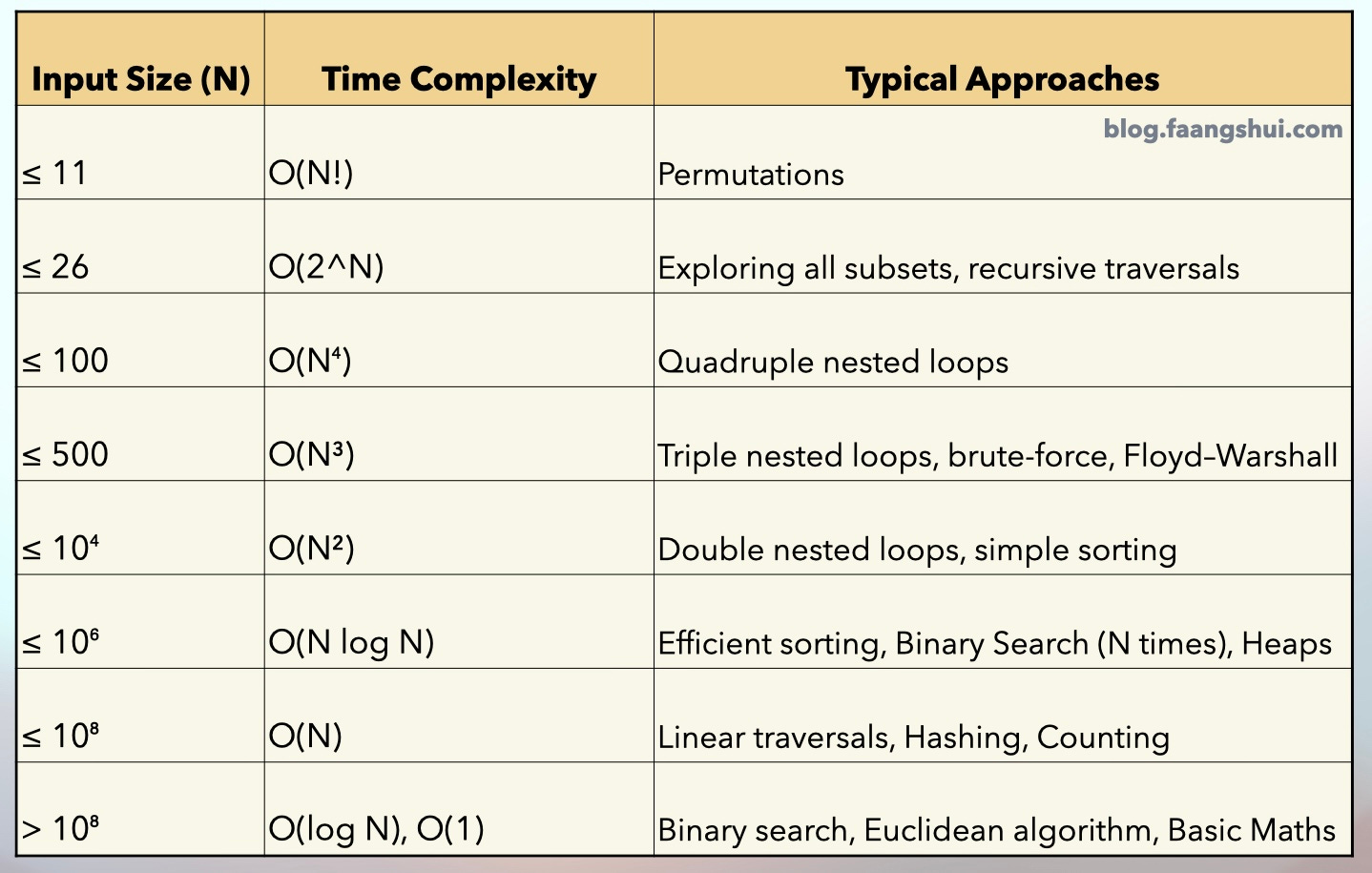
To make it easier for you, I’ve compiled the following table of input sizes mapped to their target time complexities. You don’t need to memorize the table. Once you know the constraints, you can easily deduce the target time complexity—just remember the key limit of 100 million operations (10^8) per test case.
This constraint-to-time-complexity analysis also works when you’re dealing with multiple variables. Just plug the maximum values into the functions describing the time complexity, and you can still figure out the target time. As long as you understand the principle of 100 million operations per test, you can quickly figure out the correct time complexity for any problem.
Now, let’s put this knowledge to the test with a couple of exercises.
Exercise 1
Problem Statement:
Given a stream of integers of length up to 10⁸, find the first non-repeating integer.
Input Constraints:
The length of the input stream N can be as large as 10⁸.
Question:
What’s the target time complexity?
Exercise 2
Problem Statement:
Given an array of intervals, merge all overlapping intervals.
Input Constraints:
The number of intervals N can be as large as 10⁵.
Question:
What’s the target time complexity?
Understanding input constraints is like reading a map—it shows you the best route to the solution. Once you master this technique, you’ll be able to make quick decisions about the time complexity and algorithmic approach for any coding challenge. Whether you’re solving for N≤10⁵ or N≤10⁸, the constraints hold the key to optimal problem-solving.
Try applying this technique in your next coding practice session. And if you found this helpful, share it with a friend preparing for their interviews.


Very informative